25-11-2023

Merge sort for noobs

As a self-taught programmer I always struggle with some programming concepts or algorithms. It might be something super simple or super complex, but the struggle is there.

So the idea of merge sort algorithm is pertty simple. You take an array of something that you want to sort and split it in half. Then, you sort each half individually and then re-combine those two halves together.

Very simple concept. The tricky thing comes from the idea that it's recursive. It means that if you split something in half, and each half have more elements to them - split again. Let's look at an example,

You have array of numbers = [0,5,3,4,1,2,6,7]

When you first split it you will get

left half = [0,5,3,4]

right half = [1,2,6,7]

And since these halves have more than 1 number we need to split and sort them as well. And this is where recursion happens. Let me take screenshot from Harvard's CS50 lecture to illustrate the algorithm.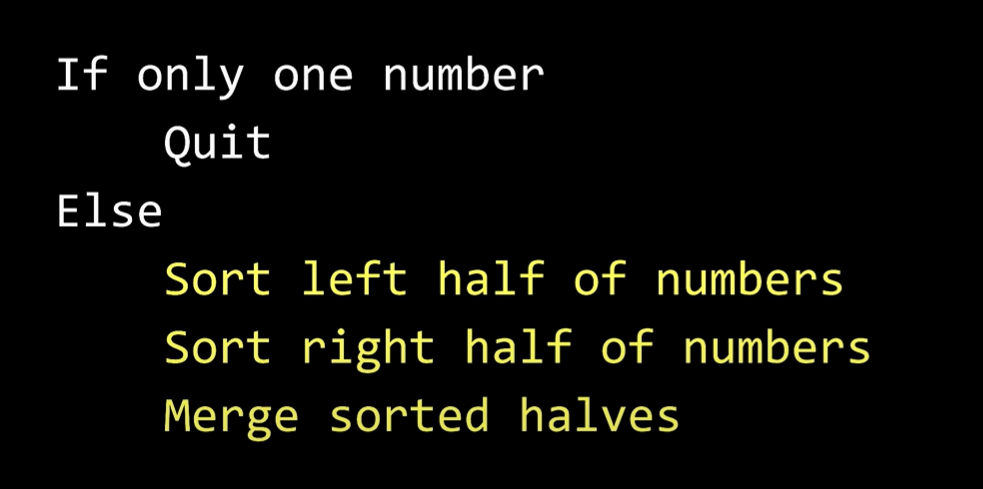

Very big point to make, that in order to do the splitting and searchin - you'd need to create new arrays. So when you do the merge sort, you allocate additional memory. Which is not the case with Quick Sort, but I will cover it another time.

Now let's code it. In the beggining let's create the merge_sort() function. This is where the main recursion is going to happen. As arguments we going to provide the array to sort (in this case an integer array) and a length of it. The length as argument comes only because C can't have dynamic arrays. In python, you wouldn't specify it.

base case when we want to stop the recursion.

now we need to find a middle point where we going to split array in two halves.

and here we define those two arrays for our split halves.

here we populate these two arrays with data from the "original" array. it's in quotations because the array that gets passed into this function during recursion will be a left or right array just from iteration previously.

this is all the work in terms of splitting arrays. now let's call the recursion. and this is where we will sort of build the order of operation on splitting. when at some point left half has only 1 element in array it will stop doing stuff, because of base case. it will go to iterate over all the right halves.

and after splitting, we call the most important function merge()

 Now this is where the real shit happens and where it becomes trippy. We need to go over each array in a sequence and compare each element to another. Let's take and example. We have two sorted arrays that we need to merge.

left half = [0,3,4,5]

right half = [1,2,6,7]

To merge them together, we need to compare each number against another and place the smallest one into final array.

is left_half[0] (0) less then right_half[0] (1)? Yes. Add it to final array.

final_array = [0]

is left_half[1] (3) less then right_half[0] (1)? No. Add right half number into final array.

final_array = [0,1]

And we continue this until we merge everyhting together. Now let's code it.

For the definition of a function we need left half array, right half array and an original array where we going to change the order of elements. And also for the sake of C, we provide length of an array.#

here we calculate the size of arrays, so we can iterate over them

now we define iterators for our arrays. we going to run a while loop and once we add an element to an array we going to +1 to the iterator.

now we go in a continious loop where we check if left iterator hasn't gotten to an end of left array and same for the right array. and within the loop we check which number is bigger.

here we cover a case when right half is all in the final array and we just need to add the remains of left array to the final array. and then the same code for the right side.

And now these are 2 functions that make the merge sort. It might seems super easy and stupid, but I had was struggling to gather my thought in one place into a good and tight code. I'm also attaching the C file that you can use.

Merge_Sort_Algorithm

I hope that this article will help someone like me who just keeps hitting their head against the wall and can't understand what's going on.

And after all of this explanation, look at this scheme where people teach this algorithm and tell me if you could learn it from THAT. I definitely wouldn't be able to.

And as a bonus, here's the python code for merge sort.

def mergeSort(array):
    if len(array) > 1:

        #  r is the point where the array is divided into two subarrays
        r = len(array)//2
        L = array[:r]
        M = array[r:]

        # Sort the two halves
        mergeSort(L)
        mergeSort(M)

        i = j = k = 0

        # Until we reach either end of either L or M, pick larger among
        # elements L and M and place them in the correct position at A[p..r]
        while i < len(L) and j < len(M):
            if L[i] < M[j]:
                array[k] = L[i]
                i += 1
            else:
                array[k] = M[j]
                j += 1
            k += 1

        # When we run out of elements in either L or M,
        # pick up the remaining elements and put in A[p..r]
        while i < len(L):
            array[k] = L[i]
            i += 1
            k += 1

        while j < len(M):
            array[k] = M[j]
            j += 1
            k += 1


# Print the array
def printList(array):
    for i in range(len(array)):
        print(array[i], end=" ")
    print()


# Driver program
if __name__ == '__main__':
    array = [6, 5, 12, 10, 9, 1]

    mergeSort(array)

    print("Sorted array is: ")
    printList(array)

Category: Coding

Comments